- 018 How to stack
- 017 Brainf___ machine
- 016 Formal verification
- 015 How to count
- 014 Connecting FPGA to a computer
- 013 Binary numeric screen mode
- 012 VESA output by FPGA
- 011 Programming Xilinx Spartan 6
- 010 Learning basics of Verilog
- 009 Improvements in the blog engine
- 008 Migrating to AWS
- 007 LCD screens
- 006 Joule thief
- 005 Hall effect sensors
- 004 Constant acceleration revisited
- 003 Digital pendulum
- 002 Driving stepper motor
- 001 Play with forth and STM32
- 000 Hello world
Constant acceleration revisited
What is wrong?
In the last article the first section is about constant acceleration... But is it really?
The rule is to change delay for each step to be e.g. 0.9 of delay for previos step. $$ \Delta t_{i+1} = 0.9 \Delta t_i $$
Continuous function that satisfies this equation is e.g. (starting from 10ms delay) $$ t' = 10 (0.9)^x $$ Which is almost equal to $$ t' = 10 e^{-{x \over 10}} $$
By integrating this with assumption that \(t(0) = 0\), we get $$ t = 100 - 100 e^{-{x \over 10}} $$ By solving for \(x\) we get $$ x = -10 \ln {{100 - t} \over 100} $$
This is not a quadratic eqaution that I expected for constant acceleration! Moreover it goes to \(\infty\) for \(x \rightarrow 100\).
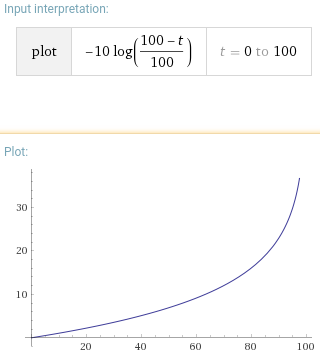
Why is that? When delay becomes shorter, we execute more steps in an unit of time. Motor accelerates with each step, so when delay becomes shorter it accelerates more quickly.
How to really get constant acceleration
Let's say we have $$ x = a t^2 $$ Solving it for \(t\) gives $$ t = \sqrt {x \over a} $$ By calculating derivative we get $$ t' = {1 \over {2 \sqrt {a x}}} $$
I calculated it in Forth as before I did for pendulum movement and now my stepper is really accelerating nicely.
As usually, source code is on GitHub.